Trigram model calculations
Recall that P(w1,n) = P(w1) P(w2|w1)
P(w3|w1,2) ... P(wn|w1,n-1).
Now assume that the probability of each word's occurrence is affected only
by the two previous words i.e.
(1) P(w1,n) = P(wn|wn-2,wn-1)
Since the first word has no preceding words, and since the second word has
only one preceding word, we have:
(2) P(w1,n) = P(w1)
P(w2|w1) P(w3|w1,2)
P(w4|w2,3) ... P(wn|wn-2,n-1)
For simplicity, suppose there are two "empty" words w0 and w-1
at the beginning of every string. Then every term in (2) will be of the
same form, referring to exactly two preceding words:
(3) P(w1,n) = P(w1|w-1,0)
P(w2|w0,1) P(w3|w1,2)
... P(wn|wn-2,n-1)
i.e.
(4) P(w1,n) = Pi=1,n
(wi|wi-2,wi-1)
We estimate the trigram probabilities based on counts from text. E.g.
(5) Pe(w1|wi-2,i-1)
= C(wi-2,i) / C(wi-2,i-1)
For example, to estimate the probability that "some" appears after "to
create":
(6) Pe(some|to create) = C(to
create some)/C(to create)
From BNC, C(to create some) = 1; C(to create) = 122, therefore Pe(some|to
create) = 1/122 = 0.0082
Probability of a string
LAST NIGHT I DREAMT I WENT TO
MANDERLEY AGAIN.
76 LAST NIGHT I P = 76/5915653 =
cat triplet_counts | grep "NIGHT I
DREAMT"
22 NIGHT I
WAS
439 I WAS GON
726 WAS GON NA
1249 GON NA BE
155 NA BE A
203 BE A BIT
1301 A BIT OF
429 BIT OF A
108 OF A SUDDEN
11 A
SUDDEN HE
...
Missing counts/back-off
A problem with equation (4) is that if any trigrams needed for the
estimation are absent from the corpus, the probability estimate Pe
for that term will be 0, making the probability estimate for the whole
string 0. Recall that a probability of 0 = "impossible" (in a grammatical
context, "ill formed"), whereas we wish to class such events as "rare" or
"novel", not entirely ill formed.
In such cases, it would be better to widen the net and include bigram and
unigram probabilities in such cases, even though they are not such good
estimators as trigrams. I.e. instead of (4) we use:
(7) P(wn|wn-2,n-1)
= λ1 Pe(wn)
(unigram probability)
+ λ2 Pe(wn|wn-1)
(bigram probability)
+ λ3 Pe(wn-2,n-1)
(trigram probability)
where λ1, λ2 and λ3 are weights. They
must add up to 1 (certainty), but assuming that trigrams give a better
estimate of probability than bigrams, and bigrams than unigrams, we want λ1
< λ2 < λ3, e.g. λ1 = 0.1, λ2
= 0.3 and λ3 = 0.6.

Are these the best numbers?
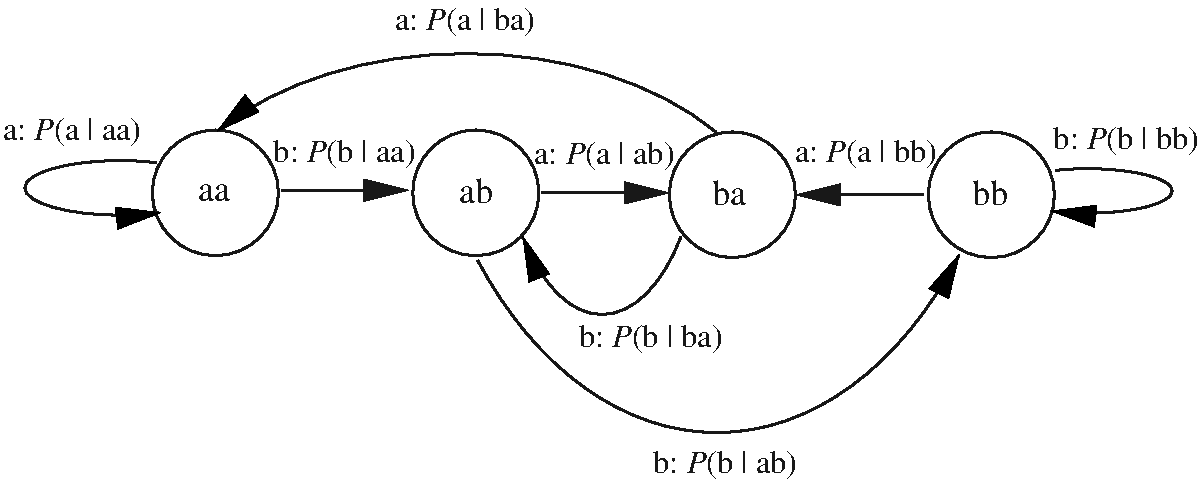
Given fig. 7.9, how might a "b" occur after seeing "ab"?
1) state sequence ab, λ1, bb P = λ1
P(b)
2) state sequence ab, λ2, bb P = λ2
P(b|b)
3) state sequence ab, λ3, bb P = λ3
P(b|ab)
Any of these routes through the graph would be possible. We do not know
which route might be taken on an actual example. We do not know, for
instance, whether we have an estimate of the trigram probability P(b|ab)
in the training corpus - sometimes we do, sometimes we do not. We want to
be able to compute the best i.e. most probable path, without necessarily
knowing which arcs are traversed in each particular case. It is because
the sequence of arcs traversed are not necessarily seen that these models
are called
hidden.

